• シンセサイザの操作で遊んだ頃＾＾；
  
• オシレータ(SynthEdit)
  
• オシレータの音量を制御
  
• エンベロープ･ジェネレータ(ADSR)を使う
  
• VCF(ボルテージ・コントロールド・フィルタ)
  
• フィルタ(ポール、レゾナンス)について
  
• フィルタの原理
  
• FFTフィルタ
• シンセサイザと楽器の表現力？
  
• 鍵盤のないシンセサイザ
  
• LFO(ロー・フリケンシ･オシレータ)
  
• SynthEditで組んだシンセサイザの一例
  
• 「ビブラート」「ワウワウ」「トレモロ」
  
• LFOのかけ具合
  
• LFOのシンクロと繰り返し
  
• ワウとエンベロープ・フォロア
  
• エンベロープ･フォロア(Peak Follower)の波形
  
• エンベロープ･フォロアの波形追いかけ度合い！？＾＾；
  
• 「ビブラート」「ワウワウ」「トレモロ」で変調＾＾；
  

以前の『フィルタ(ポール、レゾナンス)について』で、ポールについて少し書きましたが、ポール数の大きいフィルタだと、キレがよく、カットオフ周波数付近で音を分離してくれたりします。そのポールってのは、フィルタの原理にあった、遅らせる音や、フィードバックする音の数と、音量の調節具合で、決まってくるのかな?^^;

でも、そういう原理のフィルタだと、ある周波数を境にキッチリと分離するということは出来なかったりするみたいですね?(多分^^;)。FIR(ファイナイト・インパルス・レスポンス)フィルタや、IIR(インフィニティ・インパルス・レスポンス)フィルタを作ったことは無いので、よく分かりませんが、やっぱり、若干の周波数域に渡った分離しか出来ないのかもしれないですね。でも、FIRやIIRという方法ではなく、FFT(ファースト･フーリエ･トランスフォーム:高速フーリエ変換)という演算を使うと、かなりキッチリと分離することができます。こんな感じです。

- FFTフィルタ -

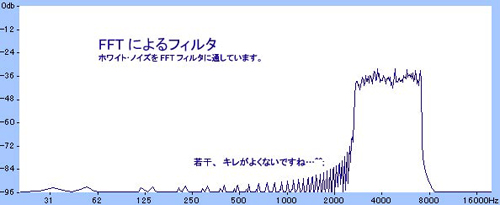
ホワイト･ノイズをFFTフィルタに通し、3000〜8000Hz付近のみを取り出しています。

図では、ホワイト･ノイズをFFTフィルタで、3000〜8000Hz付近を取り出しています。

音というのは、時間経過に伴う振幅の変化だったりしますが、エフェクタのディレイやリバーブ、またフィルタでは、振幅を変化させたり、先のFIRやIIRのように、時間操作をすることで、音に変化を与えてます。でも、FFTは、ちょっと違ってたりします^^;。勿論、FFTも「時間経過に伴う振幅の変化」をしている「音」を扱いますが、FFTの複雑な演算を行うと、一定幅の周波数ごと(0〜20Hz、20〜40Hz…といった感じ)に音の大きさが求まります。周波数域ごとに音を扱うことが出来れば、カットオフ周波数を境に、高音低音の音を分離することは簡単ですね。FFTを使ったロー･パス･フィルタだと、カットオフ周波数以上の音の大きさを0にすればいいですよね。物凄いキレのよいフィルタですね^^;

ところで、先の図のように、横軸が周波数で、縦軸が音量となっているものがありますけども、それは、FFTを使っているんです^^。周波数域毎の音の大きさを算出して、グラフ上に描いているんです。因みに、算出したものを音に戻すには、IFFT(インバース・ファースト･フーリエ･トランスフォーム:逆高速フーリエ変換)という演算をするそうですよ^^;