• 偶数倍音列と奇数倍音列の音について
• 偶数奇数倍音列の各音の周波数比
  
• 偶数倍音列と奇数倍音列の音
  
• 偶関数＋奇関数でのウェーブシェーピング
  

前回「波形に変化を与える(偶数倍音を自在に２)」では、正規分布の式を使ってウェーブシェーピングし、偶数倍音の数を自在に変化させるということでしたが、これで、奇数倍音も偶数倍音も自在に作り出せるようになりました^^。

- ちょっとブレイク - KORGから面白そうなシンセサイザが出るみたいですね。 「40年以上の歳月に渡り電子楽器を作り続けてきたコルグならではのノウハウ、アイディアを惜しみなく投入。さらに高剛性アルミ・フレーム構造を大胆に採用した、まったく新しいフォルムをまとったコルグ渾身の一作」 だそうです。 モジュールタイプのシンセサイザを使っている人とかは分かりやすいかもです。 KORG　RADIAS/RADIAS-R

奇数倍音については、このモジュールで、



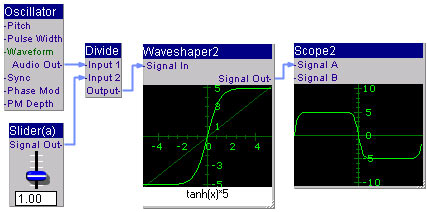
- ウェーブシェーピング「tanh(x/a)*5」のモジュールを組む -

数式「tanh(x/a)*5」のx/aの部分を「Waveshaper2」の前で処理しています。 図は、数式「tanh(x/a)*5」においてa=0.1とした時のウェーブシェーピングとなっています。 左端の「Scope2」は、ウェーブシェーピング後の波形です。 オシレータは、440Hzサイン波を出力しています。

また、偶数倍音については、前回「波形に変化を与える(偶数倍音を自在に２)」のこのモジュールで発生させることができるので、

- 正規分布の式「exp(-a*x^2)*10-5」でモジュールを組み、aを変えた時の偶数倍音の発生具合 -

上がモジュール図で下がaを変えた時の倍音発生の周波数分布図です。 サイン波440Hzをウェーブシェーピングしています。 aの値を大きくすると高次に渡って倍音を発生します。 「Waveshaper2」の入力の制限は、-5〜5なのですが、数式「exp(-1*x^2)*10-5」の線が 制限外のx＜-5、x＞5の時も、x=-5、x=5の時とほぼ同じ値になるので、ウェーブシェーピングには 問題なかったりします(多分^^;)

これらのモジュールを並行して使うといいかもしれないですね^^;

ところで、440Hzを基音とした時の倍数列は、こんな感じになります(実際、倍音の周波数は、鍵盤の音程からズレがあったりします)。

- 440Hzの倍音と音程についての図 -

数値は周波数です。 白と黒の縦棒は、鍵盤つもりです^^; 黄色い丸は440Hz、赤色は、偶数倍音、青色は奇数倍音です。 おおよその図になっています。

奇数倍音列では、基音を「ラ」とした時、順に「ミ(1)、ド♯(2)、ミ(2)、ソ(2)、シ(3)…」(括弧内の数はオクターブ上という意味で書いています^^;)の音階に近くなり、偶数倍音列では、順に「ラ(1)、ラ(2)、ミ(2)、ラ(3)、ド♯(3)…」です。奇数倍音は、基音「ラ」以外の音階を含んでいますが、偶数倍音は「ラ」が多かったりしますね。色んな音階が混じると、音はうねりを発生して濁ったりします。因みに、うねりがあると、耳に引っかかったり、目立つ音に感じるみたいですね。

実際は、先ほども書いたように、音階から少しズレがあるので、周波数を見てみると、基音を440Hz(ラ)とした時、奇数倍音列は順に「1320、2200、3080、3960、4840Hz…」で、偶数倍音列は「880、1760、2640、3520、4400Hz」となります。ところで、1オクターブ内の音階で、濁りの最も少ない組み合わせは、オクターブだと思うのですが、例えば「ラ」とオクターブ上の「ラ」(周波数比1:2=0.5)、「ラ」と5度上の「ミ」(周波数比2:3=0.6666…純正律の場合)だと、前者には濁りを感じなかったりします。

偶数倍音列では、各音のオクターブが、その倍音列に含まれてたりするんですよね。例えば、1つ目の880Hzのオクターブ上の音は、倍の1760Hzとなりますが、これは、2つ目の周波数と同じですよね。なので、この2つの音の間には、濁りが無かったりします。また、2つ目の1760Hzの倍は3520Hzで、これは4つ目の倍音と同じですよね。一方、奇数倍音列では、1つ目の1320Hzのオクターブ上の音は2640Hzですが、これは倍音列にないですよね。ということで、両者の音に違いがあったりするんです。