前回「波形に変化を与える(ウェーブシェーピング７)」では、数式「5*sin(x/PI)」の曲線の膨らみを更に、膨らますということで、”数式「5*sin(x/PI)」のxに、同じく数式「5*sin(x/PI)」を代入する”ということを紹介しました。その数式は「5*sin(5*sin(x/PI)/PI)」となって、その曲線は、数式「5*sin(x/PI)」のものより、直線「y=x」を基準として膨らみました(右肩上がりの線の傾きが大きくなったというか…^^;)。これでサイン波をウェーブシェーピングすると、こんな感じになります。

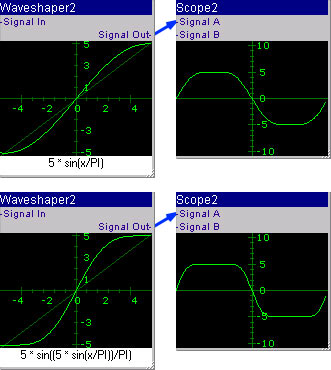
- 数式「5*sin(x/PI)」の曲線にさらに膨らみをつけた時のウェーブシェーピング後のサイン波の波形 -

上が数式「5*sin(x/PI)」でサイン波をウェーブシェーピングした時です。 下が数式「5*sin(5*sin(x/PI)/PI)」でサイン波をウェーブシェーピングした時です。 曲線の膨らみが増した分、サイン波も横方向に膨らみが出てきています。

どちらもサイン波が横方向に膨らんでますが、数式「5*sin(x/PI)」より、数式「5*sin(5*sin(x/PI)/PI)」でウェーブシェーピングしたサイン波の方が、より膨らんでいます。後者の波形の山の頂上(?^^;)や谷の平らになった部分が、横方向により広くなったという感じで、四隅が直角に近い四角形になってきましたね。

数式「5*sin(x/PI)」での波形の変化で新たに奇数倍音が加わったということを以前書きましたが(参考「波形に変化を与える(ウェーブシェーピング３)」)、さらに曲線の膨らみが増した、数式「5*sin(5*sin(x/PI)/PI)」ではどうなるのか?ということで、周波数分布を調べてみると、こんな感じになりました。

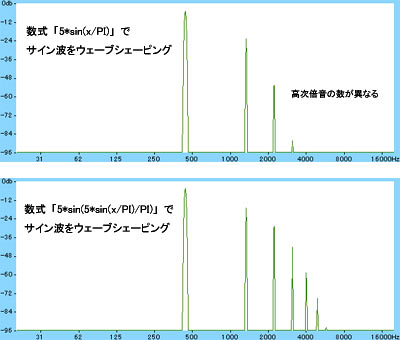
- 数式「5*sin(x/PI)」と数式「5*sin(5*sin(x/PI)/PI)」でサイン波をウェーブシェーピングした時の周波数分布 -

上が数式「5*sin(x/PI)」でサイン波をウェーブシェーピングした時です。 下が数式「5*sin(5*sin(x/PI)/PI)」でサイン波をウェーブシェーピングした時です。 数式「5*sin(5*sin(x/PI)/PI)」の方が多くの高次の奇数倍音を発生しています。