これまで、数式「5*sin(x/PI)」を中心にウェーブシェーピングを紹介してきました。そして、これにもう一つの変数を加えることで、その曲線の膨らみを変える所まで来ましたが、それは、倍音の減る方向にしか変化させることが出来なかった…ということでした^^;。次第に多くの倍音を加えていくようにするには、この数式では少々無理があるみたいですね^^;。曲線の膨らみを徐々に変えると、自然に高次の倍音が加わり、音の輝きが増してくるという感じにできると嬉しいかもですね^^;

ところで、少し話しを戻して、サイン波のウェーブシェーピングにおいて、数式を直線「y=x」から曲線「5*sin(x/PI)」に換えると、奇数倍音を発生するようになりましたが、そこから、曲線の膨らみを増やした数式「5*sin(5*sin(x/PI)/PI)」に換えると、さらに多くの奇数倍音を発生するということでした。 参考1(曲線の膨らみ)

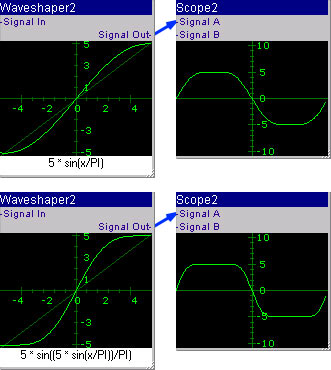
- 数式「5*sin(x/PI)」の曲線にさらに膨らみをつけた時のウェーブシェーピング後のサイン波の波形 -

上が数式「5*sin(x/PI)」でサイン波をウェーブシェーピングした時です。 下が数式「5*sin(5*sin(x/PI)/PI)」でサイン波をウェーブシェーピングした時です。 曲線の膨らみが増した分、サイン波も横方向に膨らみが出てきています。

参考2(倍音構成)

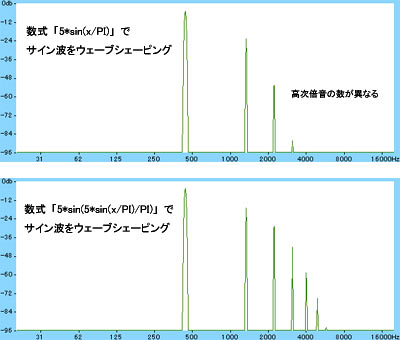
- 数式「5*sin(x/PI)」と数式「5*sin(5*sin(x/PI)/PI)」でサイン波をウェーブシェーピングした時の周波数分布 -

上が数式「5*sin(x/PI)」でサイン波をウェーブシェーピングした時です。 下が数式「5*sin(5*sin(x/PI)/PI)」でサイン波をウェーブシェーピングした時です。 数式「5*sin(5*sin(x/PI)/PI)」の方が多くの高次の奇数倍音を発生しています。

ということは、「y=x」の直線の膨らみのない状態から、線の膨らみを増やしていくと倍音の方も、だんだん増えていくってことなんですよね。そして、その線は、(x,y)=(-5,-5)、(x,y)=(0,0)、(x,y)=(5,5)を必ず通らなければならないってこともあったりします。なので、究極には、x＜0の範囲で、y=-5となって、x＞0の範囲で、y=5となるような、それに近いところまで線の膨らみが増えるといいのかもしれないですね^^;

そういう条件を満たすもので、他に、数式「5*sin(x/PI)」みたいに変化するものはないのか?ってことで、調べてみると、tanhやexp等があったりします^^;。tanhだと「tanh(x/a)*5」という感じの数式にして、aの値を0.05〜4ぐらいの間で変化させると、曲線の膨らみが大きくなったり小さくなったりします(aを3、1、0.1にした時、こんな感じに曲線が変わります)。

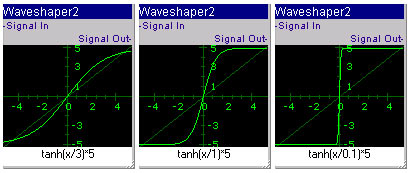
- 数式「tanh(x/a)*5」において、aを3、1、0.1とした時の「Waveshaper2」上の曲線 -

数式「tanh(x/a)*5」において、aを3、1、0.1とした時の「Waveshaper2」上の曲線です。 曲線の膨らみ具合が次第に変わっています。 (x,y)=(-5,-5)、(x,y)=(0,0)、(x,y)=(5,5)を満たしている感じですね^^;